Perbedaan Antara Centroid Circumcenter Incenter and Orthocenter | Centroid vs Circumcenter vs Incenter vs Orthocenter

Circumcenter, Incenter, Orthocenter vs. Centroid

Circumcenter: circumcenter adalah titik persimpangan tiga garis tegak lurus dari segitiga . Circumcenter adalah pusat lingkaran circumcircle , yang merupakan lingkaran yang melewati ketiga simpul segitiga.

Untuk menggambar circumcenter buat dua bilah tegak lurus ke sisi segitiga. Titik persimpangan memberi circumcenter. Sebuah bisektor dapat dibuat dengan menggunakan kompas dan ujung lurus dari penggaris. Atur kompas ke radius, yang lebih dari separuh panjang segmen garis. Kemudian buat dua busur di kedua sisi segmen dengan ujung sebagai pusat busur. Ulangi prosesnya dengan ujung segmen yang lain. Keempat busur tersebut menciptakan dua titik persimpangan di kedua sisi segmen. Gambarkan garis yang menghubungkan kedua titik ini dengan bantuan penggaris, dan itu akan memberi garis lurus pada segmen ini.

Untuk membuat circumcircle, gambar lingkaran dengan circumcenter sebagai pusat dan panjang antara circumcenter dan vertex sebagai jari-jari lingkaran.

Incenter: Incenter adalah titik perpotongan dari tiga angle bisector s. Incenter adalah pusat lingkaran dengan lingkar yang memotong ketiga sisi segitiga.

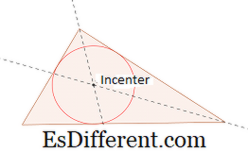
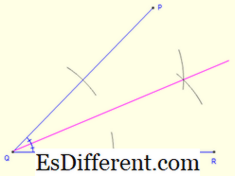
Untuk menggambar incenter segitiga, buat dua garis sudut segitiga . Titik persimpangan dari dua sudut bisectors memberi incenter. Untuk menggambar garis sudut, buat dua busur pada masing-masing lengan dengan radius yang sama. Ini menyediakan dua titik (satu di setiap lengan) di lengan sudut. Kemudian mengambil setiap titik di lengan sebagai pusat, menggambar dua busur lagi. Titik yang dibangun oleh persimpangan kedua busur ini memberi titik ketiga. Sebuah garis yang menghubungkan titik sudut dan titik ketiga memberi garis sudut.

Untuk membuat incircle , buat segmen garis tegak lurus ke sisi manapun, yang melewati incenter. Mengambil panjang antara dasar tegak lurus dan incenter sebagai jari-jari, menggambar lingkaran yang lengkap.

Orthocenter: Orthocenter adalah titik persimpangan tiga ketinggian (ketinggian) segitiga.

Untuk membuat orthocenter, gambar dua ketinggian segitiga . Segmen garis tegak lurus terhadap sisi yang melewati titik balik disebut tinggi.Untuk menggambar garis tegak lurus yang melewati sebuah titik, tandai pertama dua busur pada garis dengan titik sebagai pusatnya. Kemudian, buat dua busur lagi dengan masing-masing titik persimpangan sebagai pusatnya. Gambarlah segmen garis yang bergabung dengan titik pertama dan titik yang akhirnya dibangun, dan garis itu memberi garis tegak lurus terhadap segmen garis dan melewati titik pertama. Titik persimpangan dua ketinggian memberikan orthocenter. Centroid adalah titik persimpangan tiga median

segitiga . Centroid membagi masing-masing median dalam rasio 1: 2, dan pusat massa seragam, lamina segitiga terletak pada titik ini. Untuk menentukan centroid, buat dua median segitiga. Untuk menciptakan median, tandai titik tengah sisi. Kemudian buatlah segmen garis yang menghubungkan titik tengah dan sudut segitiga yang berlawanan. Titik persimpangan median memberi sentroid segitiga. Apa perbedaan antara Circumcenter, Incenter, Orthocenter dan Centroid?

• Circumcenter dibuat dengan menggunakan garis-garis tegak lurus dari segitiga.

• Insiden dibuat menggunakan sudut bisectors dari segitiga.

• Orthocenter dibuat dengan menggunakan ketinggian (ketinggian) segitiga.

• Centroid dibuat menggunakan median segitiga.

• Baik circumcenter maupun incenter memiliki lingkaran terkait dengan sifat geometris tertentu.

• Centroid adalah pusat geometris

segitiga, dan merupakan pusat massa laminar segitiga seragam. • Untuk segitiga non sepihak, circumcenter, orthocenter, dan centroid terletak pada garis lurus, dan garisnya dikenal sebagai garis Euler

.