Perbedaan Antara Seri Daya dan Seri Taylor
Seri Power vs Taylor Series
Dalam matematika, urutan sebenarnya adalah daftar bilangan real. Secara formal, ini adalah fungsi dari himpunan bilangan natural ke himpunan bilangan real. Jika a n adalah urutan n th , kita menunjukkan urutan oleh atau oleh a 1 , a 2 , …, a n, …. Misalnya, perhatikan urutan 1, ½, ⅓, …, 1 / n , …. Hal ini dapat dilambangkan sebagai {1 / n}.
Mungkin untuk menentukan rangkaian menggunakan urutan. Serangkaian adalah jumlah dari urutan urutan. Oleh karena itu, untuk setiap urutan, ada urutan yang terkait dan sebaliknya. Jika {a n} adalah urutan yang dipertimbangkan, maka rangkaian yang dibentuk oleh urutan tersebut dapat direpresentasikan sebagai:
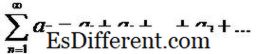
Jadi, dalam contoh di atas, seri yang terkait adalah 1+ 1 + 2 / 3 + … + 1 / n + …. Seperti namanya, rangkaian daya adalah jenis seri khusus dan digunakan secara luas dalam Analisis Numerik dan pemodelan matematika terkait. Seri Taylor adalah rangkaian kekuatan khusus yang memberikan alternatif dan cara manipulasi yang mudah untuk mewakili fungsi yang terkenal.
Apa itu seri Power?
Seri daya adalah serangkaian bentuk
yang konvergen (mungkin) untuk beberapa interval yang terpusat pada
c
. Koefisien a n dapat bilangan real atau kompleks, dan tidak bergantung pada x; saya. e. variabel dummy. Misalnya, dengan menetapkan a
n = 1 untuk setiap n, dan c = 0, rangkaian daya 1 + x + x 2 + … + x n + … diperoleh. Mudah untuk mengamati bahwa ketika x ε (-1, 1), rangkaian daya ini menyatu menjadi 1 / (1-x).
= c. Nilai lain dari x yang rangkaian kekuatannya konvergen akan selalu berbentuk interval terbuka yang terpusat pada c. Itu, akan ada nilai 0≤ R ≤ ∞ sehingga untuk setiap x memuaskan | xc | ≤ R, rangkaian daya konvergen dan untuk masing-masing x memuaskan | xc |> R, rangkaian daya berbeda. Nilai ini R disebut radius konvergensi rangkaian daya (R dapat mengambil nilai nyata atau tak berhingga positif).


seperti istilah ditambahkan atau dikurangkan bersama. Juga, memungkinkan untuk mengalikan dan membagi dua rangkaian kekuatan dengan menggunakan identitas,
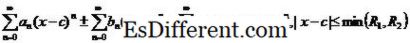
deret Taylor didefinisikan untuk fungsi f

(
x) yang tak terhingga terdiferensialkan pada interval. Asumsikan f (x) terdiferensialkan pada interval yang terpusat pada c. Kemudian rangkaian kekuatan yang diberikan oleh

x) tentang c. (Disini f (n) (c ) menunjukkan turunan n th pada x = c). Dalam Analisis Numerik, sejumlah terbatas istilah dalam ekspansi tak terbatas ini digunakan dalam menghitung nilai pada titik di mana rangkaian tersebut konvergen dengan fungsi aslinya. Suatu fungsi f (x) dikatakan analitik dalam interval (a, b), jika untuk masing-masing x ε (a, b), deret Taylor f (x) menyatu dengan fungsi f (x). Sebagai contoh, 1 / (1-x) bersifat analitik pada (-1, 1), karena ekspansi Taylor 1 + x + x 2 + … + x n + … konvergen ke fungsi pada interval itu, dan e x bersifat analitik di mana-mana, karena rangkaian Taylor e x menyatu dengan e x < untuk setiap bilangan real x. Apa perbedaan antara seri Power dan seri Taylor? 1. Seri Taylor adalah kelas khusus seri daya yang didefinisikan hanya untuk fungsi yang terdiferensiasi tak terbatas pada beberapa interval terbuka. 2. Serial Taylor mengambil bentuk spesial
sedangkan seri daya bisa berupa rangkaian bentuk




